Measurement of Halstead Metrics
with Testwell CMT++ and CMTJava (Complexity Measures Tool)
Testwell CMT++ and CMTJava are Code Complexity Measurement Tools for C, C++, Java, and C#.
The tools show Halstead-Metrics.
The tools show Halstead-Metrics.
1 Purpose and Origin
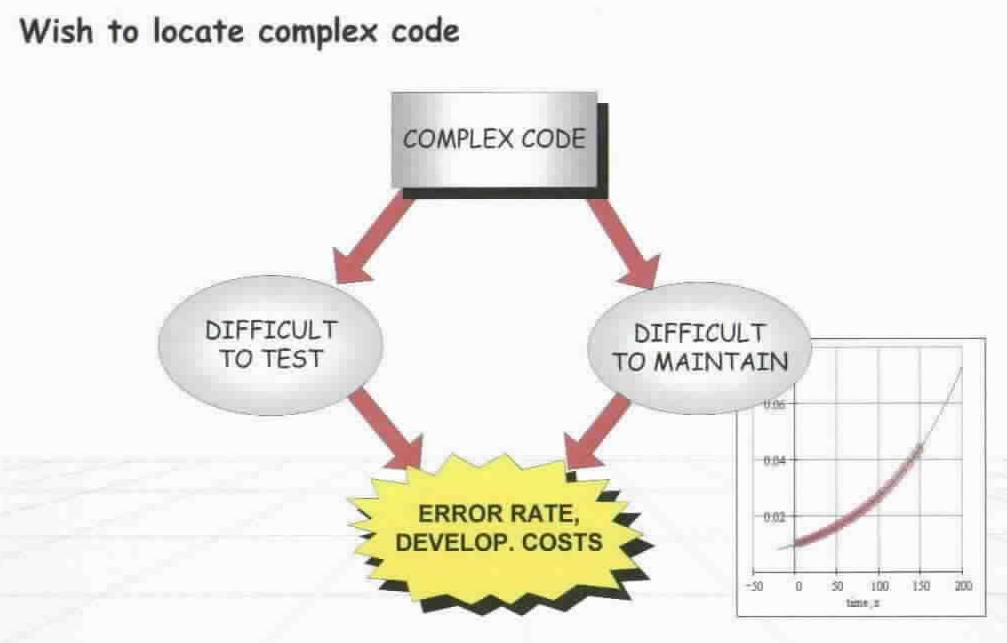
Halstead complexity metrics were developed by the late Maurice Halstead as a means of determining a quantitative measure of complexity directly from the operators and operands in the module to measure a program module's complexity directly from source code. Among the earliest software metrics, they are strong indicators of code complexity. Because they are applied to code, they are most often used as a maintenance metric. There is evidence that Halstead measures are also useful during development, to assess code quality in computationally-dense applications. Because maintainability should be a concern during development, the Halstead measures should be considered for use during code development to follow complexity trends. Halstead measures were introduced in 1977 and have been used and experimented with extensively since that time. They are one of the oldest measures of program complexity.2 Number of Operators and Operands
Halstead´s metrics is based on interpreting the source code as a sequence of tokens and classifying each token to be an operator or an operand.Then is counted
- number of unique (distinct) operators (n1)
- number of unique (distinct) operands (n2)
- total number of operators (N1)
- total number of operands (N2).
2.1 Operands
Tokens of the following categories are all counted as operants by CMT++:IDENTIFIER all identifiers that are not reserved words
TYPENAME
TYPESPEC (type specifiers) Reserved words that specify type: bool, char, double, float, int, long, short, signed, unsigned, void. This class also includes some compiler specific nonstandard keywords.
CONSTANT Character, numeric or string constants.
2.2 Operators
Tokens of the following categories are all counted as operators by CMT++ preprocessor directives (however, the tokens asm and this are counted as operands):SCSPEC (storage class specifiers) Reserved words that specify storage class: auto, extern, inlin, register, static, typedef, virtual, mtuable.
TYPE_QUAL (type qualifiers) Reserved words that qualify type: const, friend, volatile.
RESERVED Other reserved words of C++: asm, break, case, class, continue, default, delete, do, else, enum, for, goto, if, new, operator, private, protected, public, return, sizeof, struct, switch, this, union, while, namespace, using, try, catch, throw, const_cast, static_cast, dynamic_cast, reinterpret_cast, typeid, template, explicit, true, false, typename. This class also includes some compiler specific nonstandard keywords.
OPERATOR One of the following: ! != % %= & && || &= ( ) * *= + ++ += , - -- -= -> . ... / /= : :: < << <<= <= = == > >= >> >>= ? [ ] ^ ^= { } | |= ~
The following control structures case ...: for (...) if (...) seitch (...) while for (...) and catch (...) are treated in a special way.
The colon and the parentheses are considered to be a part of the constructs. The case and the colon or the for (...) if (...) switch (...) while for (...) and catch (...) and the parentheses are counted together as one operator.
2.3 Other
OPERATOR The comments delimited by /* and */ or // and newline do not belong to the set of C++ tokens but they are counted by CMT++.3.1 Program length (N)
The program length (N) is the sum of the total number of operators and operands in the program:N = N1 + N2
3.2 Size of vocabulary (n)
The vocabulary size (n) is the sum of the number of unique operators and operands:n = n1 + n2
3.3 Program volume (V)
The program volume (V) is the information contents of the program, measured in mathematical bits. It is calculated as the program length times the 2-base logarithm of the vocabulary size (n):V = N * log2(n)
Halstead's volume (V) describes the size of the implementation of an algorithm. The computation of V is based on the number of operations performed and operands handled in the algorithm. Therefore V is less sensitive to code layout than the lines-of-code measures.
The volume of a function should be at least 20 and at most 1000. The volume of a parameterless one-line function that is not empty; is about 20. A volume greater than 1000 tells that the function probably does too many things.
The volume of a file should be at least 100 and at most 8000. These limits are based on volumes measured for files whose LOCpro and v(G) are near their recommended limits. The limits of volume can be used for double-checking.
3.4 Difficulty level (D)
The difficulty level or error proneness (D) of the program is proportional to the number of unique operators in the program.D is also proportional to the ration between the total number of operands and the number of unique operands (i.e. if the same operands are used many times in the program, it is more prone to errors).
D = ( n1 / 2 ) * ( N2 / n2 )
3.5 Program level (L)
The program level (L) is the inverse of the error proneness of the program.I.e. a low level program is more prone to errors than a high level program.
L = 1 / D
3.6 Effort to implement (E)
The effort to implement (E) or understand a program is proportional to the volume and to the difficulty level of the program.E = V * D
3.7 Time to implement (T)
The time to implement or understand a program (T) is proportional to the effort. Empirical experiments can be used for calibrating this quantity. Halstead has found that dividing the effort by 18 give an approximation for the time in seconds. T = E / 18
3.8 Number of delivered bugs (B)
The number of delivered bugs (B) correlates with the overall complexity of the software.Halstead gives the following formula for B:
B = ( E ** (2/3) ) / 3000 ** stands for "to the exponent"
"Halsteads delivered Bugs" (B) is an estimate for the number of errors in the implementation.
Delivered bugs in a file should be less than 2. Experiences have shown that, when programming with C or C++, a source file almost always contains more errors than B suggests. The number of defects tends to grow more rapidly than B.
When dynamic testing is concerned, the most important Halstead metric is the number of delivered bugs. The number of delivered bugs approximates the number of errors in a module. As a goal at least that many errors should be found from the module in its testing.
4 Other "CMT"-metrics mentionned in this document
LOCproLOCpro is a Line-of-Code Metric, which shows the number of program lines (declarations, definitions, directives, and code)
more about Lines-of-Code metrics.
v(G)
v(G) McCabe's Cyclomatic number shows the complexity of the flow of control through a piece of code. v(G) is the number of conditional branches in the flowchart.
more about McCabe Metrics.
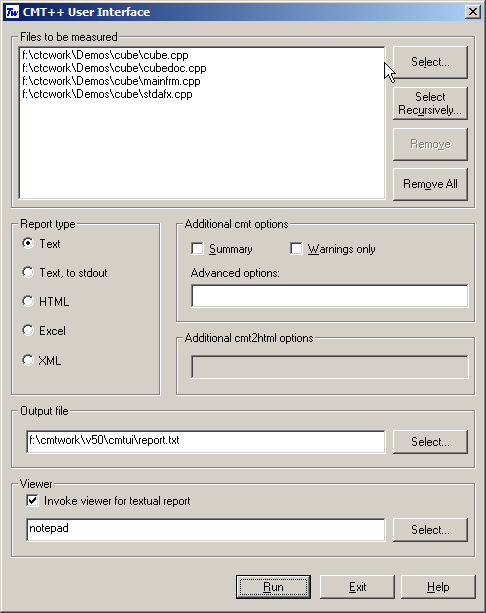
Testwell CMT++ and CMTJava analyse your applications for the following metrics:
Imagix 4D
Besides Testwell CMT++ and CMTJava Verifysoft Technology offers following tool which measures Software Complexity:We support you in order to choose the most suitable tool for you
Contact us now!